- Agua vs. tierra
- Superficie
- Volumen de Agua
- Porcentaje de agua por origen
- Porcentaje de agua por salinidad
- Agua no oceánica
- Superficie terrestre
- Atmósfera
- El Sol
- Equilibrio térmico de la Tierra
- Energía entrante
- Constante solar
- Energía total que llega a la Tierra
- Energía que llega a la superficie
- Energía emitida
- Efecto invernadero
Puedes desplegar el código si estás interesado en R.
Las librerías utilzadas son las siguientes:
Agua vs. tierra
Superficie
Configuración previa de la librería rnaturalearth, una interface para R que accede a los datos vectoriales y ráster de Natural Earth.
Utilizando los valores por defecto se genera un mapa que utiliza el esferoide WGS 84, el que se utiliza en los GPSs, y la proyección UTM, que produce distoriones entre áreas y no es buena para visualizar una comparación entre superficies, en este caso entre las de tierra y mar.
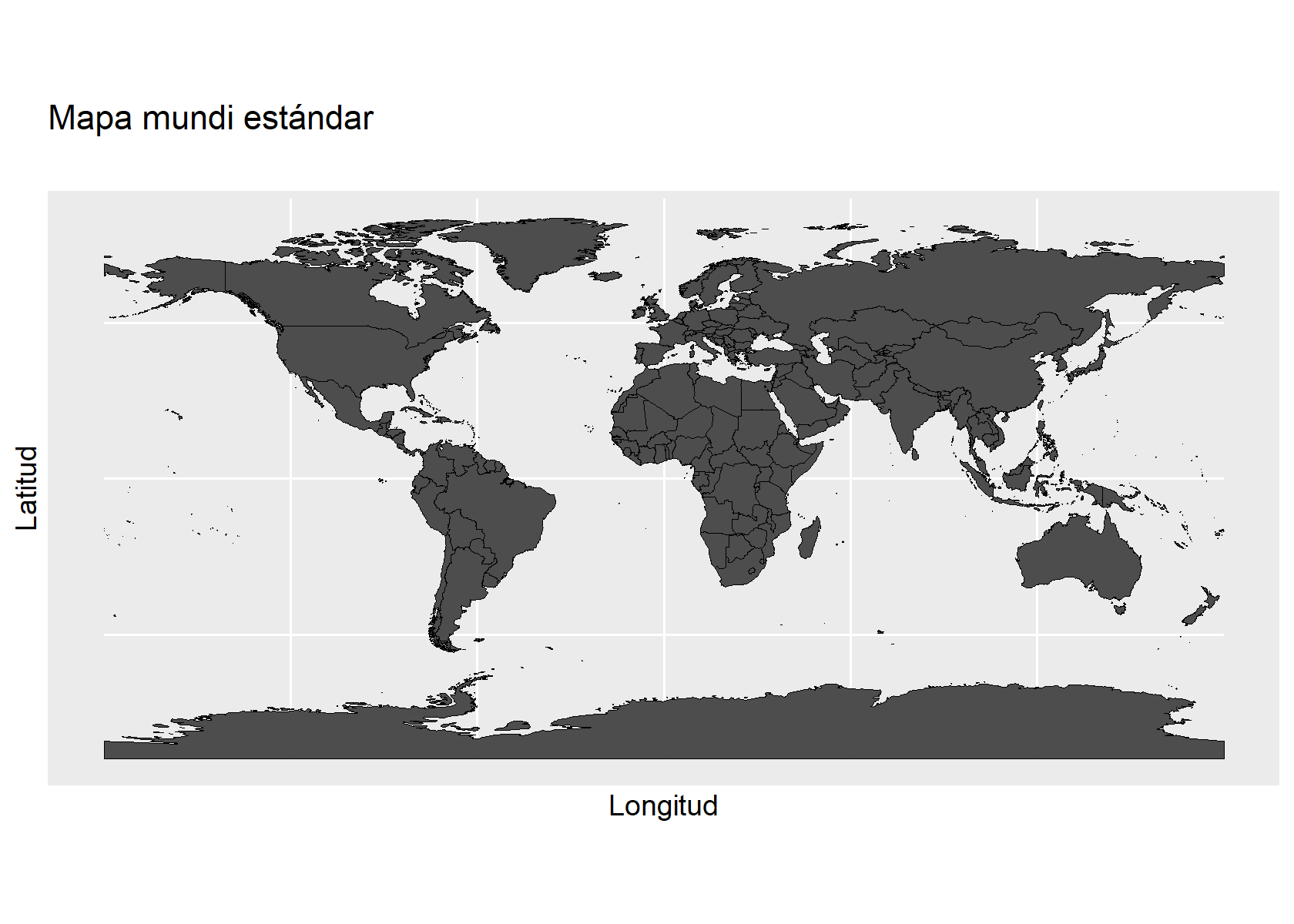
Mejor si usamos la proyección acimutal de Lambert que si conserva las áreas (aunque produce distorsiones en los ángulos).
m1 <- ggplot(data = world) +
geom_sf(color = "black", fill = "grey30", size = 0.1) +
coord_sf(crs = "+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +units=m +no_defs ")
m2 <- ggplot(data = world) +
geom_sf(color = "black", fill = "grey30", size = 0.1) +
coord_sf(crs = "+proj=laea +lat_0=-128 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +units=m +no_defs ")
m3 <- ggplot(data = world) +
geom_sf(color = "black", fill = "grey30", size = 0.1) +
coord_sf(crs = "+proj=laea +lat_0=-52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +units=m +no_defs ")
m4 <- ggplot(data = world) +
geom_sf(color = "black", fill = "grey30", size = 0.1) +
coord_sf(crs = "+proj=laea +lat_0=128 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +units=m +no_defs ")
grid.arrange(m1,m2,m3,m4, ncol = 2)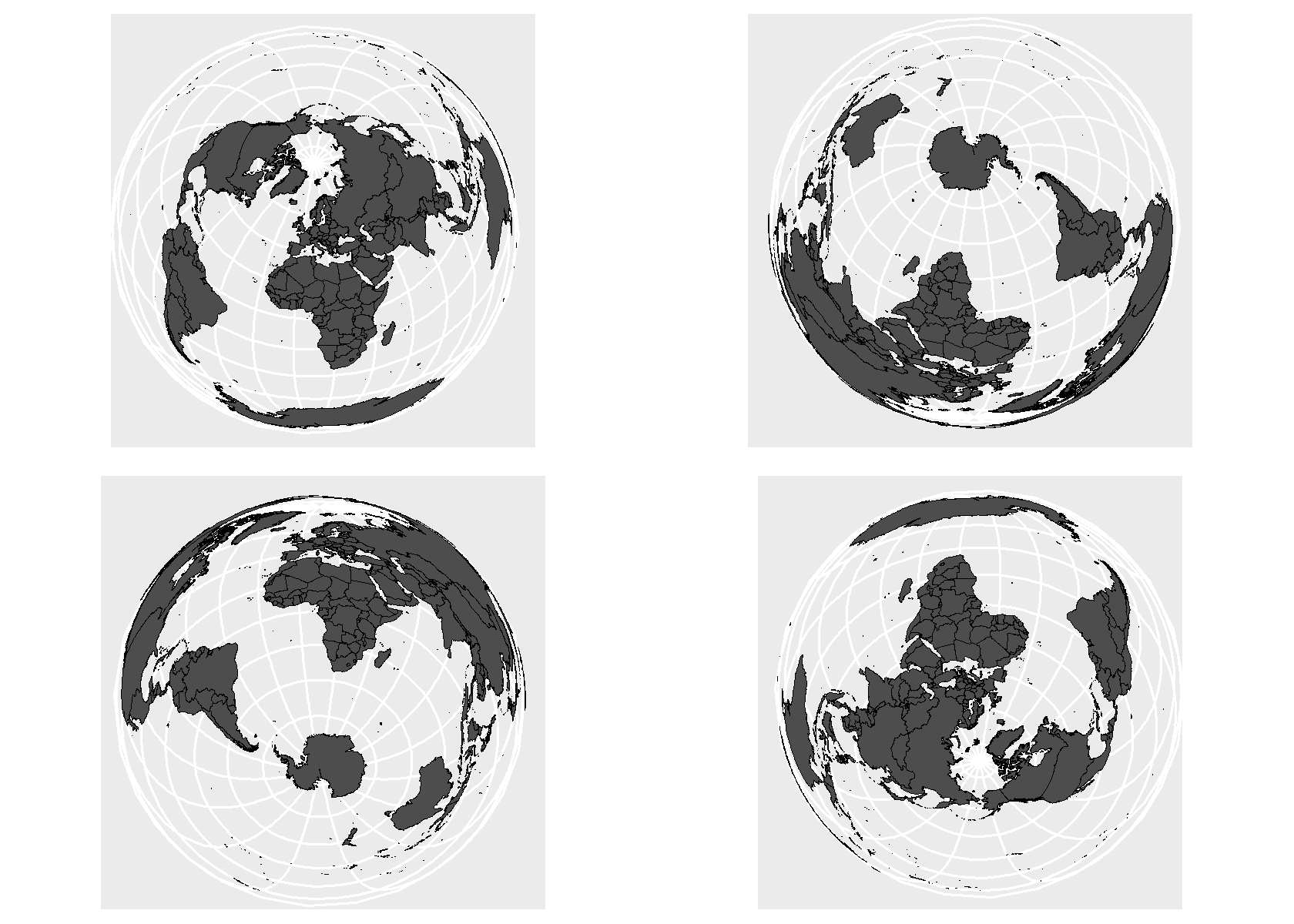
Creo que con esta proyección resulta más fácil apreciar el porcentaje que se maneja habitualmente:
el 71% de la superficie del planeta es agua.
Visto en un diagrama circular:
# Datos
data <- data.frame(
group = c("Agua", "Tierra"),
value = c(71,29)
)
# Posición de las etiquetas
# library(dplyr)
data <- data %>%
arrange(desc(group)) %>%
mutate(prop = value / sum(data$value) *100) %>%
mutate(ypos = cumsum(prop)- 0.5*prop )
# Diagrama
ggplot(data, aes(x = "", y = value, fill = group)) +
geom_bar(stat = "identity", width = 1) +
coord_polar("y", start = 0) +
theme_void() +
theme(legend.position = "none") +
geom_text(aes(y = ypos, label = group), color = "#02b83b", size = 6) +
scale_fill_manual(values = c("grey", "grey30"))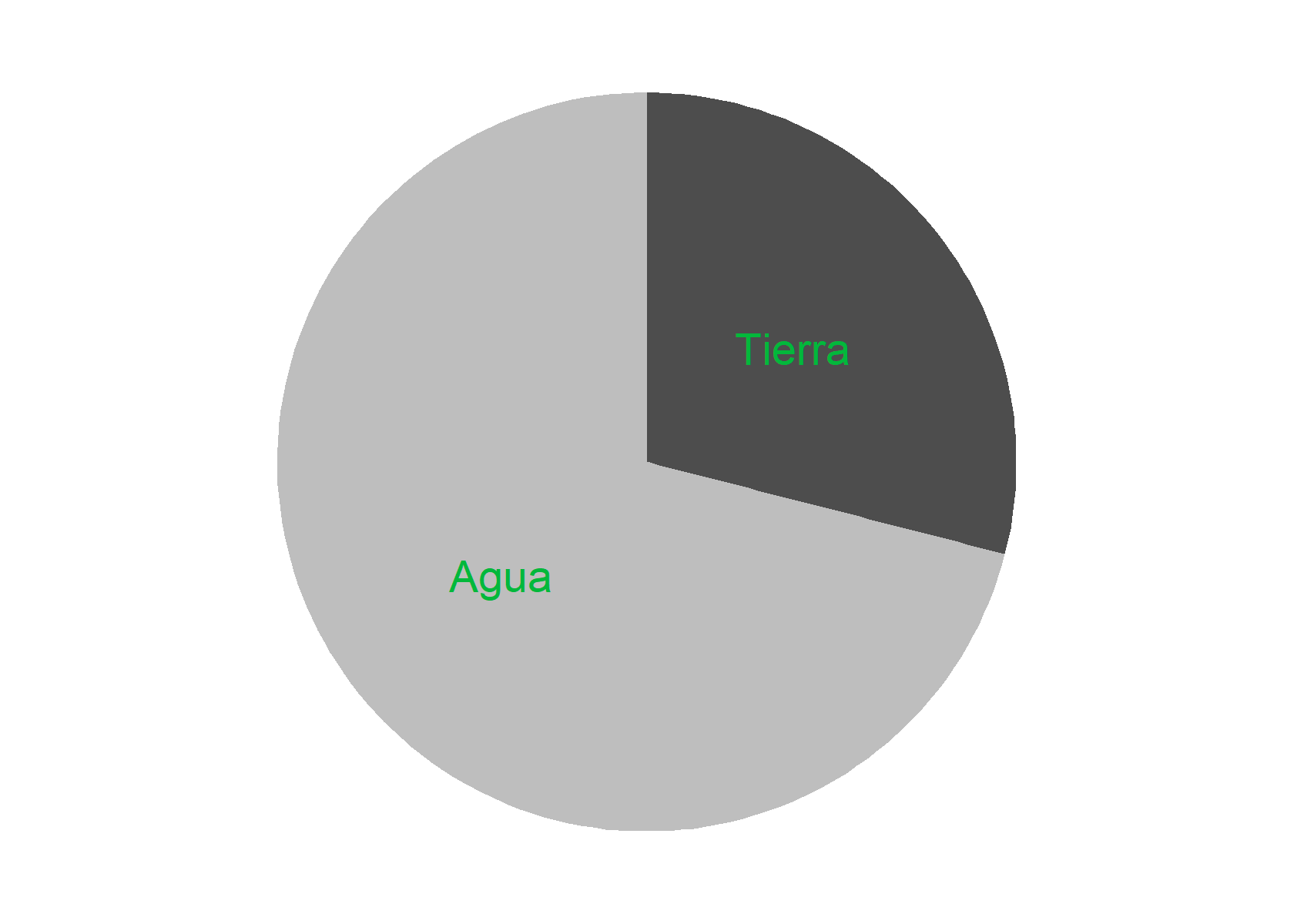
Volumen de Agua
Los datos vienen de esta página de la NASA: How Much Water is There on Earth?, me he limitado a traducir la tabla que aparece al final y a simplificarla un poco (la puedes consultar o descargar en este gist). Esto es lo que queda.
La suma de los porcentajes no es el 100% exacto debido a los redondeos, no hay nada raro ahí.
Echemos un ojo a estos valores en unos gráficos de columnas:
Porcentaje de agua por origen
Agua <- as.data.frame(Agua)
a <- ggplot(data = Agua, aes(x = reorder(Agua$Origen, -Agua$Porcentaje_Total),
y = Agua$Porcentaje_Total)) +
geom_bar(stat = "identity",fill = "steelblue") +
theme(text = element_text(size = 12, family = "Verdana Pro"),
axis.text.x = element_text(angle = 60, hjust = 1, color = "blue"),
axis.text.y = element_text(colour = "blue"),
axis.title.x = element_text(colour = "darkblue"),
axis.title.y = element_text(colour = "darkblue"),
plot.background = element_rect(fill = "#cbd0d4"),
) +
geom_text(aes(label = Agua$Porcentaje_Total), vjust = -0.25) +
xlab("Origen") +
ylab("Porcentaje") + ggtitle("", subtitle = NULL) +
coord_cartesian(clip = 'off')
# coord_flip() # queda peor
ggsave("aguaxorigen.png")
print(a)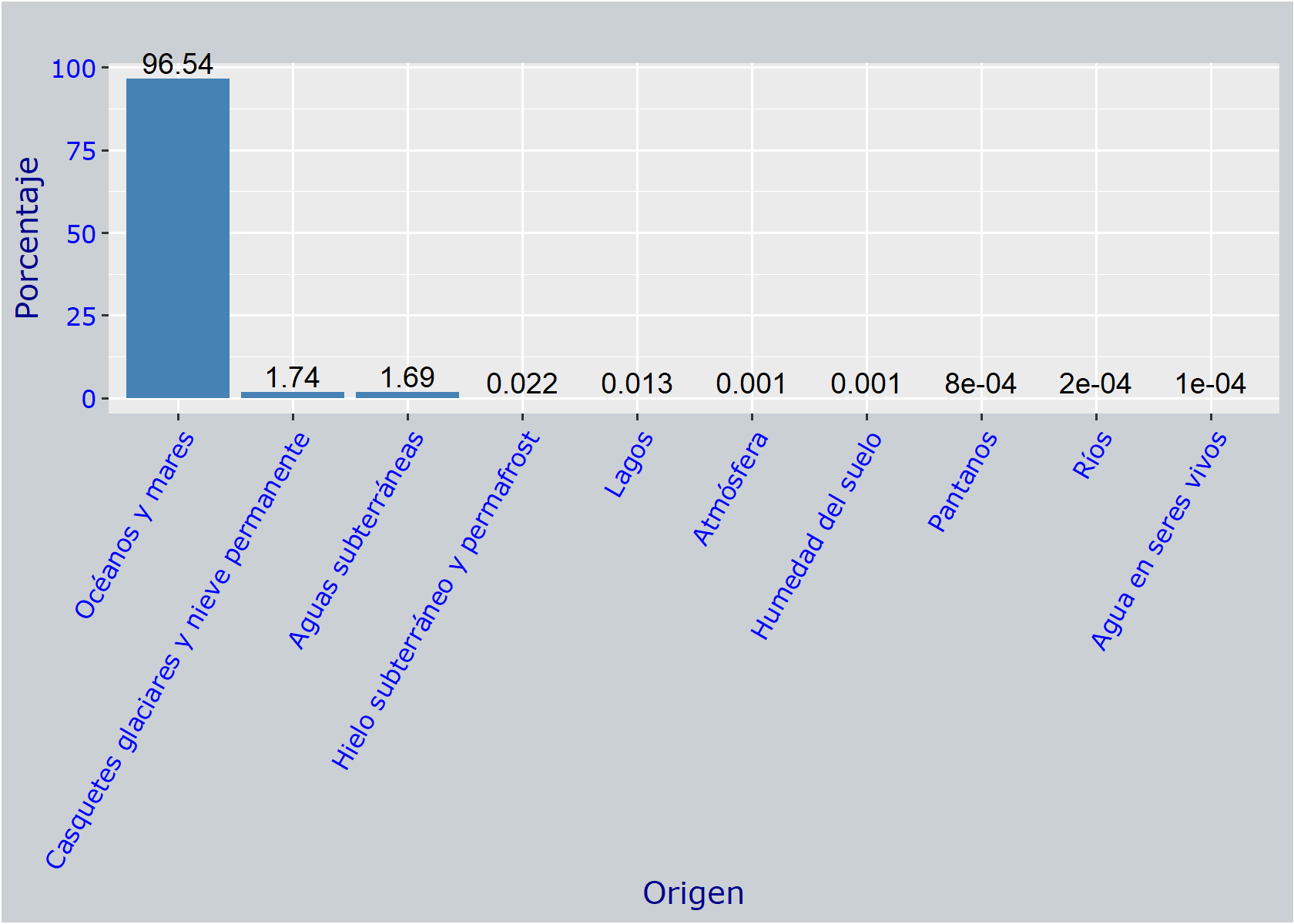
Porcentaje de agua por salinidad
Agua <- as.data.frame(Agua)
b <- ggplot(data = Agua, aes(x = reorder(Agua$Origen, -Agua$Porcentaje_Dulce),
y = Agua$Porcentaje_Dulce)) +
geom_bar(stat = "identity",fill = "steelblue") +
theme(text = element_text(size = 12, family = "Verdana Pro"),
axis.text.x = element_text(angle = 75, hjust = 1, color = "blue"),
axis.text.y = element_text(colour = "blue"),
axis.title.x = element_text(colour = "darkblue"),
axis.title.y = element_text(colour = "darkblue"),
plot.background = element_rect(fill = "#cbd0d4"),
) + ylim(0,100) +
geom_text(aes(label = Agua$Porcentaje_Dulce), vjust = -0.25) +
xlab("Origen") +
ylab("Porcentaje agua dulce") + ggtitle("", subtitle = NULL) +
coord_cartesian(clip = 'off')
ggsave("aguaxdulce.png")
print(b)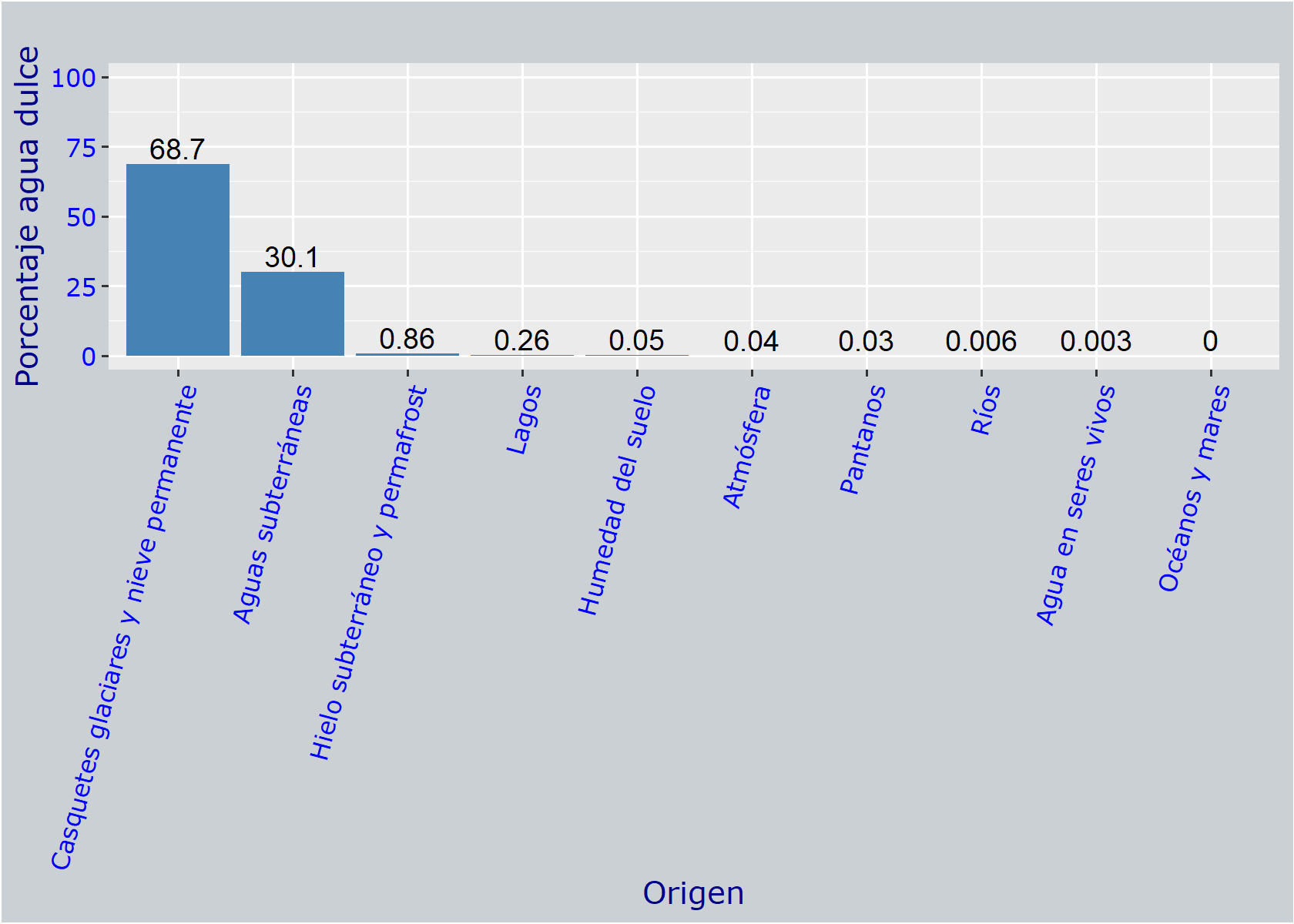
Agua no oceánica
Los casquetes glaciares, la nieve permanente y las aguas subterránes son la mayor parte del agua no oceánica:
Agua <- read.csv("AguaEnLaTierra_t.csv", encoding="UTF-8")
c <- ggplot(Agua[-1,], aes(area = Volumen, fill = Porcentaje_Total, label = Origen)) +
geom_treemap() +
theme(legend.position = "bottom") +
geom_treemap_text(fontface = "italic", colour = "white", place = "centre", grow = TRUE)
ggsave("agua.png")
print(c)
Y el resto, que aparece en oscuro en el gráfico anterior (todo por debajo del 0.03%) se distribuye de la siguiente manera:
Agua <- read.csv("AguaEnLaTierra_t.csv", encoding="UTF-8")
d <- ggplot(Agua[4:10,], aes(area = Volumen, fill = Porcentaje_Total, label = Origen)) +
geom_treemap() +
# scale_fill_brewer(palette = "Spectral") +
# scale_colour_gradientn(colours=rainbow(10)) +
theme(legend.position = "") +
geom_treemap_text(fontface = "italic", colour = "white", place = "centre", grow = TRUE)
ggsave("agua.png")
print(d)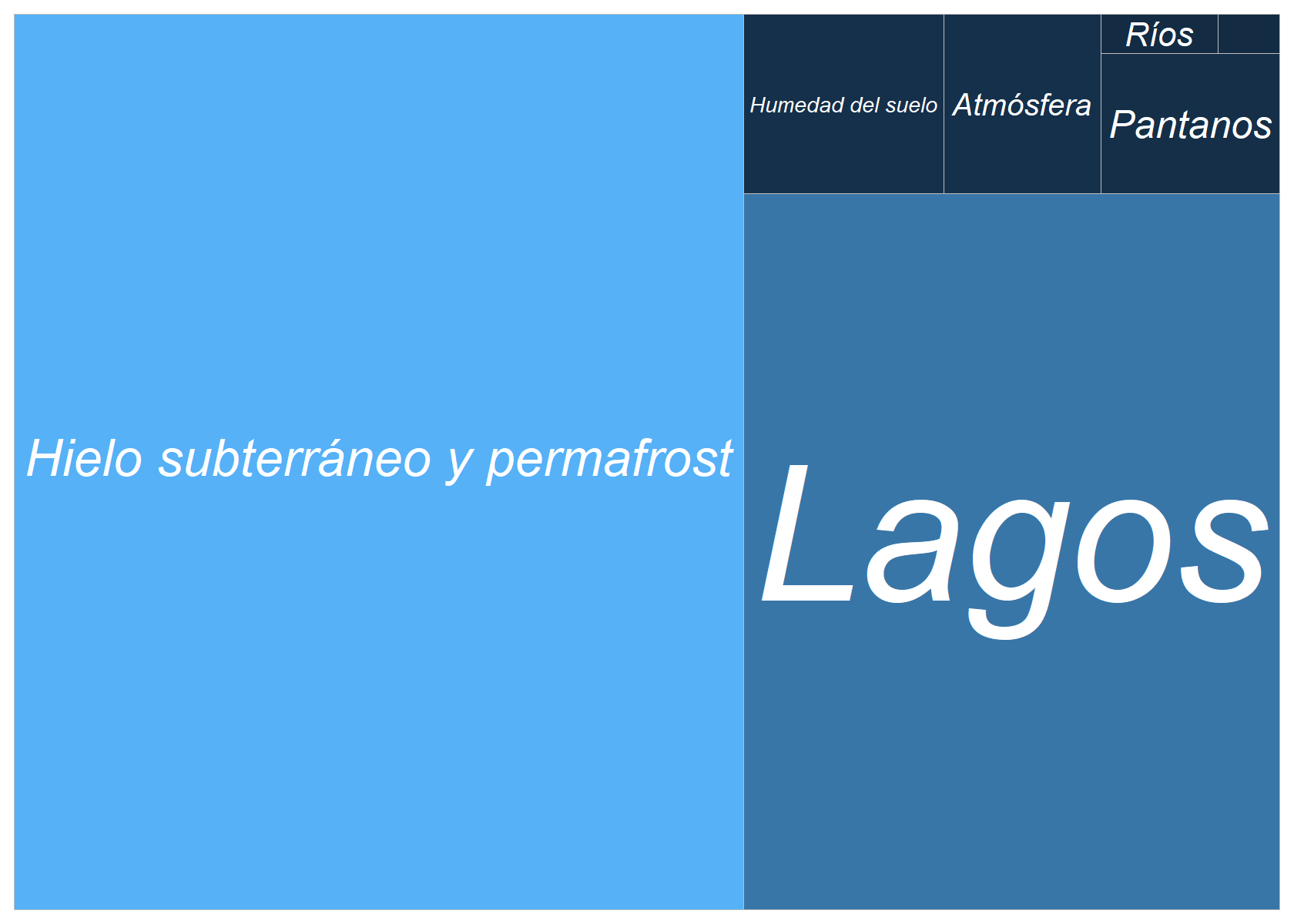
Sale oscurecida la parte que representa el menor reservorio de agua dulce del planeta, el agua de los seres vivos, que con un 0.003% (3 vasos de cada 100000), supone la mitad que todos los ríos del planeta.
Superficie terrestre
Atmósfera

Sunset on the Indian Ocean as seen by astronauts aboard the ISS
La atmósfera es una parte esencial del planeta por diferentes razones. Pero no tengo escrito nada consistente de momento. Para leer una introducción sencilla se puede visitar este enlace de la NASA que es de donde sale la foto anterior.
Adicionalmente, he seleccionado algunos esquemas y capturas de la red que tenía de hace años cuando repasé el tema, suelo compilar este tipo de recursos como presentaciones para consumo interno, sin más pretensiones que las de tener a mano las esencias y algunos enlaces. Creo que pueden ser una buena introducción, y por eso comparto aquí en PDF.
Como digo son capturas no pensadas para ser publicadas, no todo contiene las referencias aunque hay enlaces a casi todo. Viene algo de la composición de la atmósfera, de física radiativa y un montón sobre la clasificación de las nubes, más que nada porque di con unos entrañables esquemas en unos cursos de Hydrology & Atmospheric Sciences de la Universidad de Arizona que me encantaron (pag. 15 a 19 del PDF).
El Sol
Prox.

Equilibrio térmico de la Tierra
Diferencia entre la energía que entra y la energía que sale de la Tierra.
Una infografía clásica es la de NASA
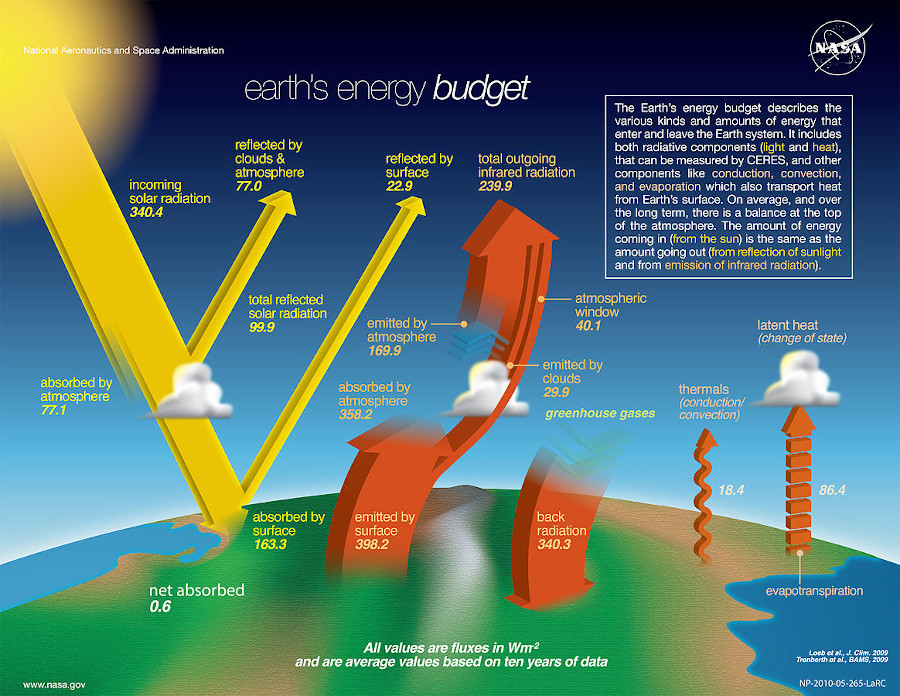
Veamos qué significan esos números.
Energía entrante
Constante solar
La energía entrante está relacionada con la constante solar, S, que se define como la energía total de la radiación recibida desde el Sol por unidad de tiempo por unidad de área en una superficie teórica perpendicular a los rayos del Sol y a la distancia media de la Tierra al Sol (a una unidad astronómica, UA ≃150 millones de kilómetros).
S=1367 W/m2
En realidad no es una constante porque el Sol no radia energía de una manera uniforme, ni tenemos un conocimiento suficiente de los procesos del sol como para modelar su comportamiento preciso y poder ofrecer un valor promedio que sirva como constante propiamente dicha (e.g. poder estimar su comportamiento durante miles de años), al menos no de una manera robusta.
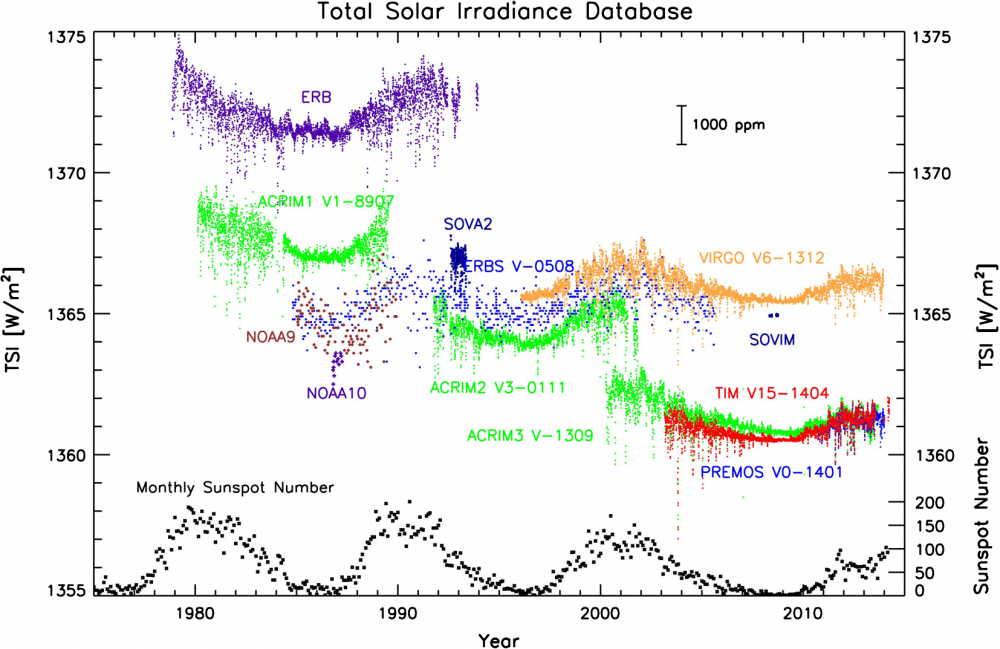
Pero eso no es ningún problema porque desde 1978 medimos por satélite de manera muy precisa la radiación total del Sol (TSI) sobre el planeta. En el siguiente gráfico se presentan las medidas por satélite desde ese año, así como un conteo (en densidad mensual) de las manchas solares.
Esto es una evidencia sólida de que el calentamiento reciente no se debe a la actividad del Sol. Pero:
No conocemos, ni podemos conocer, la actividad solar antes de 1978 con una resolución comparable a la que hoy medimos. Las reconstrucciones pueden ser más o menos relevantes, pero están constreñidas por limitaciones inherentes que las hacen inservibles como modelos robustos del pasado. Aunque se manejan registros de manchas solares desde el 800
a. C.no empiezan a ser fiables hasta el sigloXVIIy el uso del telescopio, como los contabilizados por el mismísimo Galileo, y posteriormente series compiladas desde el sigloXVIIIhasta la actualidad (que son a menudo re-compiladas -en el momento de escribir esto la versión2.0de julio de 2015), o series específicas de un acontecimiento como el mínimo de Maunder, interesantes en el debate por su coincidencia con la Pequeña Edad de Hielo, que podría ser un punto que muestra la importancia del comportamiento del sol, más allá de sus conocidos ciclos de 11 años (que se pueden apreciar fácilmente en el gráfico anterior), aunque parece un punto más retórico que fáctico porque todo aquí es revisable, de nuevo, no conocemos todavía todo lo necesario para sacar conclusiones campanudas.El Sol no influye en el Clima exclusivamente a través de la energía irradiada, su campo magnético, o sus variaciones, son esenciales en la regulación de las partículas que llegan a éste planeta, singularmente porque son esenciales en los procesos de nucleación relacionados con las nubes y otros procesos atmosféricos. Pero hay líneas de investigación en este sentido, aunque suelen ser ignoradas y despreciadas en los medios -ver por ejemplo este hilo de Twitter si se me permite la auto cita.
Energía total que llega a la Tierra
Considerando un disco de superficie A=πR2T, tendríamos que la potencia media que nos llega del sol es:
PM=S×A=S×πR2T
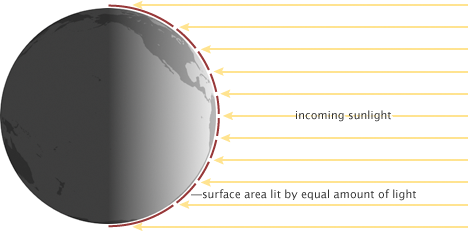
Nota. Se considera la superficie de un disco (πR2T) en vez de la superficie de una esfera (4πR2T), porque es una forma de promediar el hecho de que sólo una cara de la Tierra recibe energía del sol (un factor 1/2), y que la energía recibida por la parte iluminada depende de la latitud (otro factor 1/2), según se puede ver en esta imagen obtenida del Earth Observatory de la NASA Climate and Earth’s Energy Budget.
Este factor 1/4 es importante, y explica porqué en los gráficos habituales no vemos la contante solar (1367 W/m2) sino un número que está alrededor de su cuarta parte (≈342 W/m2), que supondría la energía recibida por la Tierra por segundo promediada en toda su superficie teniendo en cuenta su rotación y la diferente insolación según su latitud.
Utilizando el radio medio de la Tierra obtenemos:
PM=1367 W/m2×π×(6.37×106m)2=1.74×1017 W
Por supuesto es un número gigantesco, son 174 PW, donde el prefijo P (peta) significa 1015, o 174000 billones de vatios, es decir:
la Tierra recibe una energía media de 174000 billones de julios cada segundo.
Nota. Queda para el lector el ejercicio de buscarle un sentido y una moral al uso de la bomba de Hiroshima (6.3×1013 J, o 63 TJ), bH, como unidad para expresar la magnitud anterior que sería equivalente a unas 2762 bH por segundo. Ni tampoco lo es para una minúscula parte de esa cantidad que supone el forzamiento radiativo producido por el CO2 sin considerar retroalimentaciones (≈2 W/m2, según el IPCC AR5) que no es más que una pequeña fracción de los 342 W/m2 que nos llegan por segundo al planeta (el 0.58 %, por ser precisos), y que según esta “unidad de medida” equivale a unas 4 bH por segundo (que es el resultado que explota este macabro gadget, y que a su vez inspira este párrafo).
Energía que llega a la superficie
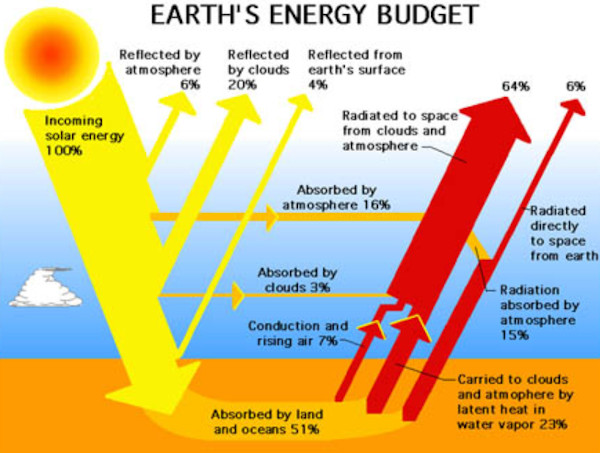
Cómo puede puede observarse en este esquema (fuente), no toda la energía que llega a la parte alta de la atmósfera (≈342 W/m2) consigue llegar a su superficie.
En números redondos. Por un lado alrededor del 30 % es reflejado por la atmósfera, el mar y, sobre todo, las nubes. Por el otro, alrededor del 20 % es absorvido por el vapor de agua, el polvo, el ozono y de nuevo las nubes, y se incorpora al flujo de energía emitida al espacio.
En resumen, de la energía por segundo que llega a un plano perpendicular a los rayos del Sol, la contante solar (1367 W/m2), estimamos que el promedio efectivo que llega al planeta es una cuarta parte (≈342 W/m2), de la que sólo el 70 % se incorpora al sistema climático terrestre (≈240 W/m2), y sólo la mitad (≈170 W/m2) es absorvido por la superficie terrestre (mar y tierra).
Estos números, aproximados pero cualitativamente correctos, sirven para tener una idea de los flujos principales de la radiación entrante a la Tierra, y conviene tenerlos en mente, o en una tabla (gist).
| Flujo solar | Magnitud (W/m2) | Porcentaje del total |
|---|---|---|
| Constante solar | 1367 | NA |
| Promedio efectivo que llega a la atmósfera | 342 | 100% |
| Se incorpora al sistema climático | 240 | 70% |
| Es absorvido por la superficie (mar y tierra) | 170 | 50% |
Energía emitida
Prox.
Efecto invernadero
Prox.